Tetraktys: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Die Tetraktys der Pythagoreer== | + | ==Die Tetraktys der Pythagoreer== |
| + | |||
Tetraktys, griechisch τετρακτύς tetraktýs „Vierheit“. So nannten die antiken Pythagoreer die vierfach wirkenden Kräfte in der Natur. Sie fanden diese Vierheit in der Arithmetik, Geometrie und in der Musiktheorie. Aus diesen Erkenntnissen leiteten sie ihr Weltbild und eine Kosmologie ab, die sie als allumfassende Weltharmonie in ihren Riten verehrten.<br> | Tetraktys, griechisch τετρακτύς tetraktýs „Vierheit“. So nannten die antiken Pythagoreer die vierfach wirkenden Kräfte in der Natur. Sie fanden diese Vierheit in der Arithmetik, Geometrie und in der Musiktheorie. Aus diesen Erkenntnissen leiteten sie ihr Weltbild und eine Kosmologie ab, die sie als allumfassende Weltharmonie in ihren Riten verehrten.<br> | ||
Die Eidesformel der Pythagoreer lautete: | Die Eidesformel der Pythagoreer lautete: | ||
| Zeile 5: | Zeile 6: | ||
welche die Quelle und Wurzel der ewig strömenden Natur enthält.“ | welche die Quelle und Wurzel der ewig strömenden Natur enthält.“ | ||
<br> | <br> | ||
| + | |||
[[Bild:pythagoras-knapp.png|thumb|400px|Pythagoras von Samos, Illustration von J. August Knapp (1853-1938) – Pythagoras hält in der rechten Hand ein Tetraeder. Am rechten Bildrand auf dem Tisch liegen Winkelmaß und Zirkel. Offensichtlich wollte Knapp die Verbindung zwischen Pythagoras und der Freimaurerei deutlich machen.]] | [[Bild:pythagoras-knapp.png|thumb|400px|Pythagoras von Samos, Illustration von J. August Knapp (1853-1938) – Pythagoras hält in der rechten Hand ein Tetraeder. Am rechten Bildrand auf dem Tisch liegen Winkelmaß und Zirkel. Offensichtlich wollte Knapp die Verbindung zwischen Pythagoras und der Freimaurerei deutlich machen.]] | ||
| + | |||
Mit demjenigen, der die Tetraktys übergab, war [[Pythagoras]] selbst gemeint. Der griechische Gelehrte und Philosoph Pythagoras von Samos lebte um 570 v. Chr. bis nach 510 v. Chr.). Die Pythagoreer waren sowohl eine Schule der Wissenschaft, als auch ein religiöser Geheimbund, lebten und wirkten im damaligen italienischen Kroton.<br> | Mit demjenigen, der die Tetraktys übergab, war [[Pythagoras]] selbst gemeint. Der griechische Gelehrte und Philosoph Pythagoras von Samos lebte um 570 v. Chr. bis nach 510 v. Chr.). Die Pythagoreer waren sowohl eine Schule der Wissenschaft, als auch ein religiöser Geheimbund, lebten und wirkten im damaligen italienischen Kroton.<br> | ||
<br> | <br> | ||
| Zeile 15: | Zeile 18: | ||
==Allgemeine Ausdeutungen in freimaurerischer Literatur== | ==Allgemeine Ausdeutungen in freimaurerischer Literatur== | ||
| + | |||
{{LPB}} | {{LPB}} | ||
zehn Punkte, in vier Reihen in Form eines gleichseitigen Dreiecks angeordnet, spielen in den Riten der Pythagoreer als heiliges Dreieck eine bedeutsame Rolle. Werden die Punkte durch Linien verbunden so entstehen neun gleiche Dreiecke. Im Eid der Pythagoreer wird auf die Tetractys als Quelle der Natur Bezug genommen (s. [[Dreieck]]). | zehn Punkte, in vier Reihen in Form eines gleichseitigen Dreiecks angeordnet, spielen in den Riten der Pythagoreer als heiliges Dreieck eine bedeutsame Rolle. Werden die Punkte durch Linien verbunden so entstehen neun gleiche Dreiecke. Im Eid der Pythagoreer wird auf die Tetractys als Quelle der Natur Bezug genommen (s. [[Dreieck]]). | ||
| − | |||
'''Ergänzung''' | '''Ergänzung''' | ||
| Zeile 31: | Zeile 34: | ||
Hierocles sagt in seinem Kommentar zu den Goldenen Versen (V, Seite 47): "Aber wie kommt Gott auf die Tetraktys? Das magst du in dem heiligen Buch, das Pythagoras zugeschrieben wird, in denen Gott als die Anzahl der Zahlen gefeiert wird lernen. Denn wenn alle Dinge durch seine ewige Dekrete existieren, ist es offensichtlich, dass in jeder Art von Dingen die Zahl von der Ursache, die sie produziert, hängt .... | Hierocles sagt in seinem Kommentar zu den Goldenen Versen (V, Seite 47): "Aber wie kommt Gott auf die Tetraktys? Das magst du in dem heiligen Buch, das Pythagoras zugeschrieben wird, in denen Gott als die Anzahl der Zahlen gefeiert wird lernen. Denn wenn alle Dinge durch seine ewige Dekrete existieren, ist es offensichtlich, dass in jeder Art von Dingen die Zahl von der Ursache, die sie produziert, hängt .... | ||
| − | |||
So viele der Jünger des Pythagoras haben das Tetraktys verehrt, dass gesagt wird, dass sie ihre feierlichsten Eide darauf ablegten, vor allem, dass der Initiation. Die genauen Worte des Eides sind in den Goldenen Verse dargelegt, und sind vom Jamblichus in seinem Leben des Pythagoras bezeichnet. | So viele der Jünger des Pythagoras haben das Tetraktys verehrt, dass gesagt wird, dass sie ihre feierlichsten Eide darauf ablegten, vor allem, dass der Initiation. Die genauen Worte des Eides sind in den Goldenen Verse dargelegt, und sind vom Jamblichus in seinem Leben des Pythagoras bezeichnet. | ||
| Zeile 48: | Zeile 50: | ||
== Der pythagoreische Eid – die ewigen Kreisläufe in der Natur == | == Der pythagoreische Eid – die ewigen Kreisläufe in der Natur == | ||
| − | |||
'''»Ich schwöre es bei Dem, der sich in unsere Seele übertragen hat, als die heilige Tetraktys, der Quelle der Natur, deren Verlauf ewig ist.«''' | '''»Ich schwöre es bei Dem, der sich in unsere Seele übertragen hat, als die heilige Tetraktys, der Quelle der Natur, deren Verlauf ewig ist.«''' | ||
| − | |||
Quelle: [http://tetraktys.de/einfuehrung-1.html Tetraktys.de] KREISLÄUFE IN DER NATUR, IHRE VIERHEIT (TETRAKTYS) UND DIE DREHMATRIX IM ZAHLENSTRAHL | Quelle: [http://tetraktys.de/einfuehrung-1.html Tetraktys.de] KREISLÄUFE IN DER NATUR, IHRE VIERHEIT (TETRAKTYS) UND DIE DREHMATRIX IM ZAHLENSTRAHL | ||
| − | |||
Bewegungen im Kosmos (altgriechisch = (Welt-)Ordnung) sind überwiegend kreisförmig. Aus ihnen resultieren auch die immer wiederkehrenden Zyklen auf unserer Erde: der Sonnenlauf entsprechend den vier Himmelsrichtungen, die vier Mondphasen und die vier Jahreszeiten. Solch ein Zyklus setzt sich aus vier relevanten Phasen zusammen: | Bewegungen im Kosmos (altgriechisch = (Welt-)Ordnung) sind überwiegend kreisförmig. Aus ihnen resultieren auch die immer wiederkehrenden Zyklen auf unserer Erde: der Sonnenlauf entsprechend den vier Himmelsrichtungen, die vier Mondphasen und die vier Jahreszeiten. Solch ein Zyklus setzt sich aus vier relevanten Phasen zusammen: | ||
| − | |||
| − | |||
[[Datei:circle-sinus-1.gif|left|]] | [[Datei:circle-sinus-1.gif|left|]] | ||
'''Aufstieg, Höhepunkt, Abstieg, Ruhephase.''' | '''Aufstieg, Höhepunkt, Abstieg, Ruhephase.''' | ||
| − | |||
Zyklische Kreisläufe auf unserer Erde sind nicht nur die unmittelbare Auswirkung von Planetenbewegungen, sondern in allen Bereichen sowohl der belebten als auch unbelebten Natur allgegenwärtig. In gewisser Weise könnte man auch die berühmte Welle-Teilchen-Dualität als 4-gliedrige Periodiziät anschaulich machen, denn auch eine Sinuswelle ist im Grunde genommen nichts weiter als ein Kreislauf, der sich in vier Abschnitte gliedert. | Zyklische Kreisläufe auf unserer Erde sind nicht nur die unmittelbare Auswirkung von Planetenbewegungen, sondern in allen Bereichen sowohl der belebten als auch unbelebten Natur allgegenwärtig. In gewisser Weise könnte man auch die berühmte Welle-Teilchen-Dualität als 4-gliedrige Periodiziät anschaulich machen, denn auch eine Sinuswelle ist im Grunde genommen nichts weiter als ein Kreislauf, der sich in vier Abschnitte gliedert. | ||
| − | |||
| − | |||
Auch die Abfolge der natürlichen Zahlen enthält exakt diese zwingend 4-gliedrige Drehmatix, sobald wir die Zahlenwertsymbole unseres Dezimalsystems durch Polygone (n-Ecke) bzw. Punktemengen ersetzen. Die Punktemenge 3 – dargestellt als Dreieck, hat zum ersten Mal die Innenwinkelsumme eines halben Kreises (180 Grad). | Auch die Abfolge der natürlichen Zahlen enthält exakt diese zwingend 4-gliedrige Drehmatix, sobald wir die Zahlenwertsymbole unseres Dezimalsystems durch Polygone (n-Ecke) bzw. Punktemengen ersetzen. Die Punktemenge 3 – dargestellt als Dreieck, hat zum ersten Mal die Innenwinkelsumme eines halben Kreises (180 Grad). | ||
Nur ein Punkt bzw. eine Ecke mehr macht aus einem halben Kreis einen Vollkreis. | Nur ein Punkt bzw. eine Ecke mehr macht aus einem halben Kreis einen Vollkreis. | ||
| − | |||
[[Datei:Vollkreise-1.gif|right|]] | [[Datei:Vollkreise-1.gif|right|]] | ||
| Zeile 78: | Zeile 71: | ||
Damit ist das '''Vier(!)-eck (Tetraktys = Vierheit)''' auch das einzige Polygon mit dieser Eigenschaft. Beim Fünfeck beträgt die Innenwinkelsumme schon 1,5 Vollkreise, beim 6-Eck 2 Vollkreise usw... | Damit ist das '''Vier(!)-eck (Tetraktys = Vierheit)''' auch das einzige Polygon mit dieser Eigenschaft. Beim Fünfeck beträgt die Innenwinkelsumme schon 1,5 Vollkreise, beim 6-Eck 2 Vollkreise usw... | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''Demzufolge beginnen alle ungeraden Punktemengen mit einem neuen nur halben Kreis bzw. Dreieck, welcher mit jedem darauf folgenden Punkt zu einem Vollkreis bzw. Viereck vervollständigt wird.''' | '''Demzufolge beginnen alle ungeraden Punktemengen mit einem neuen nur halben Kreis bzw. Dreieck, welcher mit jedem darauf folgenden Punkt zu einem Vollkreis bzw. Viereck vervollständigt wird.''' | ||
| Zeile 92: | Zeile 76: | ||
'''Die "abschließende" Zahl ist also immer eine gerade Zahl.''' | '''Die "abschließende" Zahl ist also immer eine gerade Zahl.''' | ||
| − | '''Zu einem vollen Kreis gehören immer zwei Punkte bzw. Zahlen:''' | + | '''Zu einem vollen Kreis gehören immer zwei Punkte bzw. Zahlen, die tatsächlich auch wieder zwei Dreiecken entsprechen, da sich mit jedem neuen Punkt auch ein neues Dreieck aufspannt:''' |
| − | |||
[[Datei:zahlensinus.gif|left|]] | [[Datei:zahlensinus.gif|left|]] | ||
| − | |||
An dieser Gesetzmäßigkeit wird u. a. auch verständlich, warum die Pythagoreer und Platoniker den ungeraden Zahlen männlich, schöpferische Eigenschaften zugeschrieben haben, den geraden Zahlen dagegen weiblich, erhaltende Eigenschaften. | An dieser Gesetzmäßigkeit wird u. a. auch verständlich, warum die Pythagoreer und Platoniker den ungeraden Zahlen männlich, schöpferische Eigenschaften zugeschrieben haben, den geraden Zahlen dagegen weiblich, erhaltende Eigenschaften. | ||
| − | + | [[Bild:hermes-double-ouroboros1.gif|thumb|304px|left| "Des Hermes Trismegistos wahrer alter Naturweg" herausgegeben von Einem achten Freijmaurer I. C. H. Mit vier Kupfern. Leipzig, bey Adam Friedrich Böhme. 1782.]] | |
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | |||
Diese Abbildung auf einer rosenkreuzerischen Publikation des 18. Jhdt. zeigt ein Symbol, welches die alchemistische Doppel-Ouroboros mit dem Freimaurersymbol von Winkelmaß und Zirkel kombiniert. Das Ouro (Schwanz) Boros (Essen) (Der den Schwanz isst) geht zurück auf die Ägypter und gegebenenfalls weiter zurück nach Babylon und den Sumerern. | Diese Abbildung auf einer rosenkreuzerischen Publikation des 18. Jhdt. zeigt ein Symbol, welches die alchemistische Doppel-Ouroboros mit dem Freimaurersymbol von Winkelmaß und Zirkel kombiniert. Das Ouro (Schwanz) Boros (Essen) (Der den Schwanz isst) geht zurück auf die Ägypter und gegebenenfalls weiter zurück nach Babylon und den Sumerern. | ||
| Zeile 117: | Zeile 94: | ||
Tatsächlich beinhalten nur die geradzahligen Polygone rechte Winkel, ungeradzahlige keinen einzigen. Denn alle Sternpolygone (entsprechend den Teilereigenschaften von Mengen), die sich in die geradzahligen Polygone bis unendlich einbeschreiben lassen, enthalten auch parallel laufende Tangenten, da nur geradzahlige Polygone Eckpunkte aufweisen, die sich gegenüber stehen. | Tatsächlich beinhalten nur die geradzahligen Polygone rechte Winkel, ungeradzahlige keinen einzigen. Denn alle Sternpolygone (entsprechend den Teilereigenschaften von Mengen), die sich in die geradzahligen Polygone bis unendlich einbeschreiben lassen, enthalten auch parallel laufende Tangenten, da nur geradzahlige Polygone Eckpunkte aufweisen, die sich gegenüber stehen. | ||
Näheres dazu in: [http://tetraktys.de/geometrie-2.html#simplex-aggregatzustand Tetraktys.de] | Näheres dazu in: [http://tetraktys.de/geometrie-2.html#simplex-aggregatzustand Tetraktys.de] | ||
| − | + | <br> | |
| − | + | <br> | |
[[Datei:yin_yang.gif|right|]] | [[Datei:yin_yang.gif|right|]] | ||
| − | + | Das Wissen um diese Drehmatrix im "Geometrie-Zahlenstrahl" macht auf eindrucksvolle Weise verständlich, warum die Pythagoreer ihre "Zahlenmystik" auf den Kosmos übertrugen.<br> | |
| − | + | <br> | |
| − | + | <br> | |
| − | Das Wissen um diese Drehmatrix im "Geometrie-Zahlenstrahl" macht auf eindrucksvolle Weise verständlich, warum die Pythagoreer ihre "Zahlenmystik" auf den Kosmos übertrugen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Auch das Yin und Yang beinhaltet zwei statische und zwei dynamische Phasen. | Auch das Yin und Yang beinhaltet zwei statische und zwei dynamische Phasen. | ||
| − | + | <br> | |
| − | + | <br> | |
== Punkt - Linie - Fläche - Körper == | == Punkt - Linie - Fläche - Körper == | ||
| Zeile 144: | Zeile 116: | ||
Diese Kreisbewegung lässt sich unterteilen in ein aktives und passives Dreieck, entsprechend | Diese Kreisbewegung lässt sich unterteilen in ein aktives und passives Dreieck, entsprechend | ||
einer Sinuskurve. Beide Dreiecke zusammen ergeben wieder ein Viereck mit der Winkelsumme eines vollen Kreises. Auch der geometrisch dargestellte Zahlenstrahl enthält eine viergliedrige Drehmatrix, welche mit Punkt Linie, Dreieck und Quadrat beginnt, um sich sodann bis unendlich mit Dreieck und Quadrat zu wiederholen. | einer Sinuskurve. Beide Dreiecke zusammen ergeben wieder ein Viereck mit der Winkelsumme eines vollen Kreises. Auch der geometrisch dargestellte Zahlenstrahl enthält eine viergliedrige Drehmatrix, welche mit Punkt Linie, Dreieck und Quadrat beginnt, um sich sodann bis unendlich mit Dreieck und Quadrat zu wiederholen. | ||
| − | |||
'''Wie aber könnte man den leeren Raum definieren, in dem all diese Kreisläufe stattfinden?''' | '''Wie aber könnte man den leeren Raum definieren, in dem all diese Kreisläufe stattfinden?''' | ||
| Zeile 194: | Zeile 165: | ||
== "Die Zehnzahl" – aus: "Von den pythagoreischen Zahlen" == | == "Die Zehnzahl" – aus: "Von den pythagoreischen Zahlen" == | ||
| − | |||
Quelle: "Die Vorsokratiker" von Wilhelm Capelle, Alfred-Kröner-Verlag Leipzig 1935 | Quelle: "Die Vorsokratiker" von Wilhelm Capelle, Alfred-Kröner-Verlag Leipzig 1935 | ||
| − | |||
'''I Zahlenlehre''' | '''I Zahlenlehre''' | ||
| Zeile 229: | Zeile 198: | ||
''[Jamblich, Theologische Zahlenlehre S. 82, | ''[Jamblich, Theologische Zahlenlehre S. 82, | ||
10 de Falco = 44 A 13]'' | 10 de Falco = 44 A 13]'' | ||
| − | |||
| − | |||
Wo dieses "Büchlein" von Speusippos geblieben ist oder ob es überhaupt noch existiert, darüber herrscht leider Unklarheit. | Wo dieses "Büchlein" von Speusippos geblieben ist oder ob es überhaupt noch existiert, darüber herrscht leider Unklarheit. | ||
| − | |||
Geometrische Darstellung des beschriebenen Sachverhalts<br> | Geometrische Darstellung des beschriebenen Sachverhalts<br> | ||
| Zeile 243: | Zeile 209: | ||
Details unter: [http://tetraktys.de/einfuehrung-6.html#quellmaterial-tetraktys Antikes Quellmaterial] und: [http://tetraktys.de/einfuehrung-3.html#bedeutung-3 Der Schlüssel zur Tetraktys] | Details unter: [http://tetraktys.de/einfuehrung-6.html#quellmaterial-tetraktys Antikes Quellmaterial] und: [http://tetraktys.de/einfuehrung-3.html#bedeutung-3 Der Schlüssel zur Tetraktys] | ||
| + | Allgemeine Einführung: | ||
| − | |||
[http://tetraktys.de/einfuehrung-1.html#bedeutung-1 Tetraktys Einführung] | [http://tetraktys.de/einfuehrung-1.html#bedeutung-1 Tetraktys Einführung] | ||
| Zeile 272: | Zeile 238: | ||
Johann Gottfried Herder war nicht der Erste, der die Wesensgleichheit beider Systeme erkannte. | Johann Gottfried Herder war nicht der Erste, der die Wesensgleichheit beider Systeme erkannte. | ||
Schon Johannes Reuchlin verglich in seinem 1494 erschienenen Werk De verbo mirifico (Über das Wunder wirkende Wort) das Tetragramm, das den Gottesnamen JHWH darstellt, mit der Tetraktys. | Schon Johannes Reuchlin verglich in seinem 1494 erschienenen Werk De verbo mirifico (Über das Wunder wirkende Wort) das Tetragramm, das den Gottesnamen JHWH darstellt, mit der Tetraktys. | ||
| − | |||
Studie über Johann Gottfried Herders Werk: | Studie über Johann Gottfried Herders Werk: | ||
| Zeile 280: | Zeile 245: | ||
ISBN-10: 3907260406 | ISBN-10: 3907260406 | ||
ISBN-13: 978-3907260401 | ISBN-13: 978-3907260401 | ||
| − | |||
[[Bild:schule-von-athen.jpg|thumb|450px|Die Schule von Athen (ital. La scuola di Atene) ist ein Fresko des Malers Raffael, das dieser von 1510 bis 1511 in der Stanza della Segnatura des Vatikans (ursprünglich der Saal für die Unterschriftsleistung in den Privaträumen des Papstes) für Papst Julius II. anfertigte. Das Bild ist Teil eines Zyklus, der neben der „Schule von Athen“, den „Parnass“, die „Disputatio“ (Erläuterung des Altarssakraments) und die „Kardinal- und die göttlichen Tugenden und das Gesetz“ darstellt. ]] | [[Bild:schule-von-athen.jpg|thumb|450px|Die Schule von Athen (ital. La scuola di Atene) ist ein Fresko des Malers Raffael, das dieser von 1510 bis 1511 in der Stanza della Segnatura des Vatikans (ursprünglich der Saal für die Unterschriftsleistung in den Privaträumen des Papstes) für Papst Julius II. anfertigte. Das Bild ist Teil eines Zyklus, der neben der „Schule von Athen“, den „Parnass“, die „Disputatio“ (Erläuterung des Altarssakraments) und die „Kardinal- und die göttlichen Tugenden und das Gesetz“ darstellt. ]] | ||
| Zeile 311: | Zeile 275: | ||
Die Überschrift lautet übersetzt: | Die Überschrift lautet übersetzt: | ||
"Das Ganze und ein Achtel", womit die Oktave gemeint ist. In den Schleifen selbst befinden sich drei weitere Begriffe: Oktave, Quinte und Quarte. | "Das Ganze und ein Achtel", womit die Oktave gemeint ist. In den Schleifen selbst befinden sich drei weitere Begriffe: Oktave, Quinte und Quarte. | ||
| − | |||
Die oberen römischen Ziffern: 6, 8, 9, 12 werden von Musiktheoretikern den ersten vier Zahlen der Obertonreihe zugeordnet. Diese stellen eine Vierheit dar: | Die oberen römischen Ziffern: 6, 8, 9, 12 werden von Musiktheoretikern den ersten vier Zahlen der Obertonreihe zugeordnet. Diese stellen eine Vierheit dar: | ||
| + | Prime (Frequenzverhältnis 1:1) | ||
| − | Oktave | + | Oktave (Frequenzverhältnis 1:2 bzw. 6:12) |
| − | Quinte | + | Quinte (Frequenzverhältnis 2:3 bzw. 6:9 und 8:12) |
| − | Quarte | + | Quarte (Frequenzverhältnis 3:4 bzw. 6:8 und 9:12) |
<br> | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | Was haben nun diese harmonikalen Verhältnisse mit dem ganz oben beschriebenen Sachverhalt im Zusammenhang mit der Menge 10 und den Dimensionssprüngen zu tun? | ||
| + | Die Antwort ist nicht ganz einfach zu verstehen und soll hier nur grob skizziert werden: | ||
| + | <br> | ||
| + | <br> | ||
| + | Das wichtigste Diagramm der Musiktheorie ist das so genannte Lambdoma. Es handelt sich dabei um ein Koordinatensystem deren X- und Y-Achse jeweils einem schlichten n-Mengenstrahl entsprechen, wobei die Koordianten die jeweiligen Quotienten ergeben. Es handelt sich dabei also um eine einfache Divisionstabelle. Sowohl die X-Y-Zahlengeraden als auch alle Positionen im Koordinatensystem können als Polygone und Sternpolygone dargestellt werden. | ||
| + | <br> | ||
| + | Auch die harmonikalen Verhältnisse: 1:2, 2:3 und 3:4 lassen sich als so genannte Gleichtonlinien in dieses Diagramm eintragen. Dabei entspricht die Gleichtonlinie der Oktave bis unendlich Sternen, die aus Linien zusammengesetzt sind, die Quinte entspricht bis unendlich Symmetrien, die sich aus Dreiecken zusammensetzen, die Quarte hingegen ist aus Quadraten zusammengesetzt. | ||
| + | <br> | ||
| + | Somit finden wir auch in der Musik die Tetraktys von Punkt, Linie, Dreieck und Quadrat. | ||
| + | Polygone und Sternpolygone sind demnach als Schwingungsform zu begreifen. | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | Das Lambdoma ist sehr alt. Albert von Thimus (1806-1878) entdeckte ein bis dahin unverstandenes Zitat in einem Kommentar von Jamblichos (neuplatonischer Philosoph 3. Jh. n. Chr.) zur kleineren Arithmetik des Nikomachos (neuplatonischer Philosoph 2. Jh. n. Chr). Dort heißt es : | ||
| + | |||
| + | "Von der Einheit aus wird von einem Winkel aus eine Figur in Gestalt des Lambda gezeichnet. Auf der einen Seite der Reihe werden die an die Einheit sich anschließenden Zahlen aufgezeichnet. Die andere Seite wird - beginnend von dem größten der Teile, welcher das seiner Größe nach dem Ganzen zunächst liegende Halbe ist - der Reihe nach mit den hieran sich anschließenden Teilen beschrieben." | ||
| + | |||
| + | Diese Hinweise, wie auch das Originalzitat ist in Hans Kayers Lehrbuch der Harmonik zu finden. | ||
| + | (Kayser, Hans; Lehrbuch der Harmonik; Zürich, Occident, 1950, S. 60) | ||
<br> | <br> | ||
<br> | <br> | ||
| − | == Siehe auch | + | == Siehe auch == |
*[[En:Tetractys]] | *[[En:Tetractys]] | ||
*[[Pythagoras]] | *[[Pythagoras]] | ||
*[[Geometrie]] | *[[Geometrie]] | ||
*[[Geometrie? Fragen & Antworten]] | *[[Geometrie? Fragen & Antworten]] | ||
| + | *[[Pentagramm]] | ||
| + | *[[Hexagramm]] | ||
*[[Harmonik]] | *[[Harmonik]] | ||
*[[Melencolia § I]] | *[[Melencolia § I]] | ||
| Zeile 338: | Zeile 325: | ||
== Links == | == Links == | ||
| − | + | *Thema "Geometrie" auf Tetraktys.de http://tetraktys.de/einfuehrung-1.html#bedeutung-1 | |
| − | *Thema "Geometrie" | ||
{{Sprachen|En:Tetractys|English}} | {{Sprachen|En:Tetractys|English}} | ||
[[Kategorie:Lexikon]] | [[Kategorie:Lexikon]] | ||
[[Kategorie:HolgerUllmann]] | [[Kategorie:HolgerUllmann]] | ||
Aktuelle Version vom 12. Mai 2019, 01:28 Uhr
Inhaltsverzeichnis
- 1 Die Tetraktys der Pythagoreer
- 2 Allgemeine Ausdeutungen in freimaurerischer Literatur
- 3 Der pythagoreische Eid – die ewigen Kreisläufe in der Natur
- 4 Punkt - Linie - Fläche - Körper
- 5 Punkt - Linie - Fläche - Körper – Die Tetraktys in Samuel Prichards "Masonry Dissected"
- 6 "Die Zehnzahl" – aus: "Von den pythagoreischen Zahlen"
- 7 Die Tetraktys in Johann Gottfried Herders Werk: Metakritik zur Kritik der reinen Vernunft, Leipzig 1799
- 8 Die Tetraktys in der Musiktheorie
- 9 Siehe auch
- 10 Links
- 11 In anderen Sprachen
Die Tetraktys der Pythagoreer
Tetraktys, griechisch τετρακτύς tetraktýs „Vierheit“. So nannten die antiken Pythagoreer die vierfach wirkenden Kräfte in der Natur. Sie fanden diese Vierheit in der Arithmetik, Geometrie und in der Musiktheorie. Aus diesen Erkenntnissen leiteten sie ihr Weltbild und eine Kosmologie ab, die sie als allumfassende Weltharmonie in ihren Riten verehrten.
Die Eidesformel der Pythagoreer lautete:
"Nein, bei dem, der unserer Seele die Tetraktys übergeben hat,
welche die Quelle und Wurzel der ewig strömenden Natur enthält.“
Mit demjenigen, der die Tetraktys übergab, war Pythagoras selbst gemeint. Der griechische Gelehrte und Philosoph Pythagoras von Samos lebte um 570 v. Chr. bis nach 510 v. Chr.). Die Pythagoreer waren sowohl eine Schule der Wissenschaft, als auch ein religiöser Geheimbund, lebten und wirkten im damaligen italienischen Kroton.
Leider sind uns kaum originale Aufzeichnungen der Pythagoreer erhalten geblieben. Relativ sichere Information stammen von Herodot (ca. 490 – 420 v. Chr.) und Platon (427 – 347 v. Chr).
Die einzigen direkten Überlieferungen pythagoreischen Gedankenguts in Bezug auf die Tetraktys finden sich in den Fragmenten des Pythagoreers Philolaos (um 450 v.Chr.): ANTIKES QUELLMATERIAL ZUR TETRAKTYS
Weitere wertvolle Hinweise finden wir in "Die Zehnzahl" – aus den Aufzeichnungen von Speusippos: "Von den pythagoreischen Zahlen", siehe weiter unten.
Allgemeine Ausdeutungen in freimaurerischer Literatur
Quelle: Internationales Freimaurer-Lexikon von Eugen Lennhoff und Oskar Posner (1932)
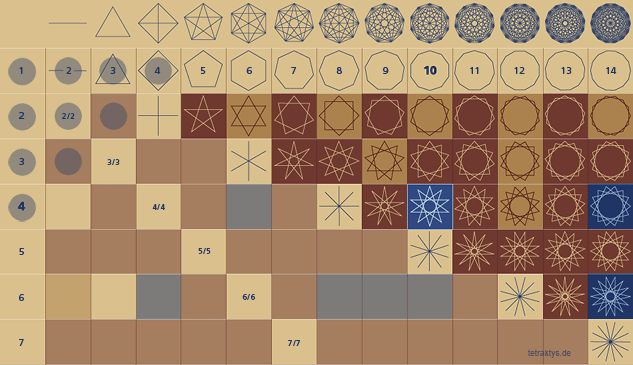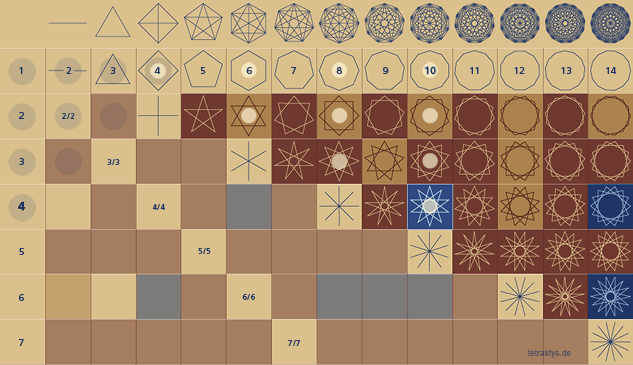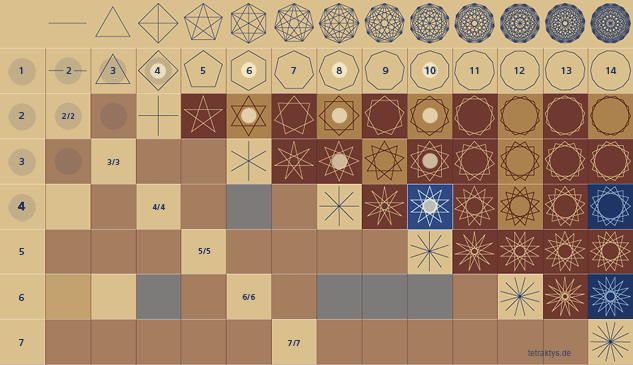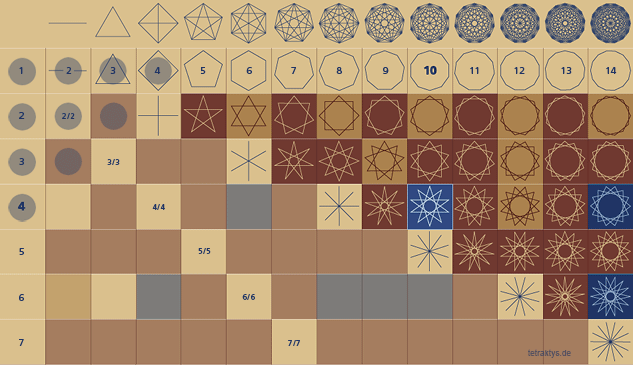
zehn Punkte, in vier Reihen in Form eines gleichseitigen Dreiecks angeordnet, spielen in den Riten der Pythagoreer als heiliges Dreieck eine bedeutsame Rolle. Werden die Punkte durch Linien verbunden so entstehen neun gleiche Dreiecke. Im Eid der Pythagoreer wird auf die Tetractys als Quelle der Natur Bezug genommen (s. Dreieck).
Ergänzung
Quelle: Mackey's Encyclopedia of Freemasonry
Das griechische Wort bedeutet wörtlich übersetzt, die Nummer 4, und steht als Synonym für Quaternation, aber es bezog sich auf ein Symbol der Pythagoreer, welches sich zusammensetzt aus zehn Punkten, die in einer dreieckigen Form angeordnet und in vier Reihen zusammengesetzt wurden.
Diese Anordnung der zehn Punkte in einer dreieckigen Form wurde die Tetraktys oder Nummer Vier genannt, weil jeder der Seiten des Dreiecks aus vier Punkten bestand, und die ganze Zahl 10 wurde von der Summation der ersten vier Zahlen gebildet, 1 + 2 + 3 + 4 = 10.
Hierocles sagt in seinem Kommentar zu den Goldenen Versen (V, Seite 47): "Aber wie kommt Gott auf die Tetraktys? Das magst du in dem heiligen Buch, das Pythagoras zugeschrieben wird, in denen Gott als die Anzahl der Zahlen gefeiert wird lernen. Denn wenn alle Dinge durch seine ewige Dekrete existieren, ist es offensichtlich, dass in jeder Art von Dingen die Zahl von der Ursache, die sie produziert, hängt ....
So viele der Jünger des Pythagoras haben das Tetraktys verehrt, dass gesagt wird, dass sie ihre feierlichsten Eide darauf ablegten, vor allem, dass der Initiation. Die genauen Worte des Eides sind in den Goldenen Verse dargelegt, und sind vom Jamblichus in seinem Leben des Pythagoras bezeichnet.
Ich schwöre es bei Dem, der sich in unsere Seele übertragen hat, als die heilige Tetraktys, der Quelle der Natur, deren Verlauf ewig ist.
Jamblichus gibt eine andere Ausdrucksweise des Eides, aber im Wesentlichen mit derselben Bedeutung.
In den Symbolen der Freimaurerei, finden wir das heilige Delta mit der nächsten Analogie zur Tetraktys der Pythagoreer. Diese Punkte die den Umriss bilden, können als ein Dreieck wahrgenommen werden. Und wenn wir kurze Wege von Punkt zu Punkt zeichnen, werden wir in diesem großen Dreieck neun kleinere finden. Doktor Hemming, in seiner 1813 erfolgten Revision der englischen Vorträge, erklärt dieses Symbol so:
Das große Dreieck wird in der Regel pythagoräisch heißen, weil es als eine prinzipielle Darstellung jenes Philosophen-Systems gedient hat. Dieses kraftvolle Emblem verdeutlicht die mystische Beziehung zwischen den numerischen und geometrischen Symbolen. Es besteht aus zehn Punkten, um ein großes gleichseitigen Dreiecks zu bilden, und ist zur gleichen Zeit so angeordnet und komponiert, um sie in neun ähnliche Dreiecke mit kleineren Abmessungen unterteilen zu können.
Die erste Einheit davon ist eine so genannte Monade, welche jeweils das Prinzip durch die Multiplikation (von denen alle Kombinationen von Form und Zahl jeweils erzeugt werden) verkörpert. Diese Monade könnte als Antworten für die Frage stehen: Was ist ein Punkt in der Geometrie?
Der pythagoreische Eid – die ewigen Kreisläufe in der Natur
»Ich schwöre es bei Dem, der sich in unsere Seele übertragen hat, als die heilige Tetraktys, der Quelle der Natur, deren Verlauf ewig ist.«
Quelle: Tetraktys.de KREISLÄUFE IN DER NATUR, IHRE VIERHEIT (TETRAKTYS) UND DIE DREHMATRIX IM ZAHLENSTRAHL
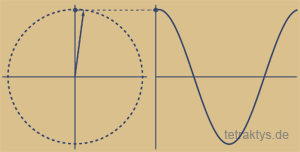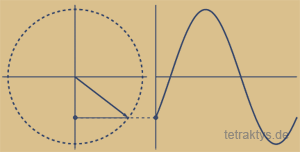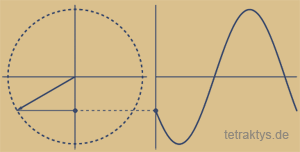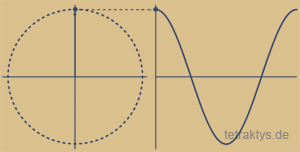
Bewegungen im Kosmos (altgriechisch = (Welt-)Ordnung) sind überwiegend kreisförmig. Aus ihnen resultieren auch die immer wiederkehrenden Zyklen auf unserer Erde: der Sonnenlauf entsprechend den vier Himmelsrichtungen, die vier Mondphasen und die vier Jahreszeiten. Solch ein Zyklus setzt sich aus vier relevanten Phasen zusammen:
Aufstieg, Höhepunkt, Abstieg, Ruhephase.
Zyklische Kreisläufe auf unserer Erde sind nicht nur die unmittelbare Auswirkung von Planetenbewegungen, sondern in allen Bereichen sowohl der belebten als auch unbelebten Natur allgegenwärtig. In gewisser Weise könnte man auch die berühmte Welle-Teilchen-Dualität als 4-gliedrige Periodiziät anschaulich machen, denn auch eine Sinuswelle ist im Grunde genommen nichts weiter als ein Kreislauf, der sich in vier Abschnitte gliedert.
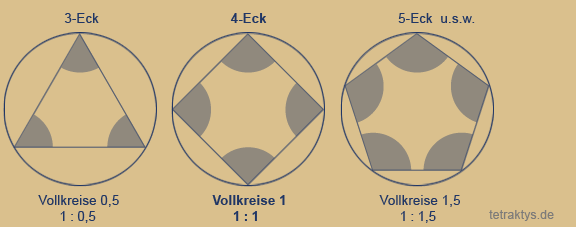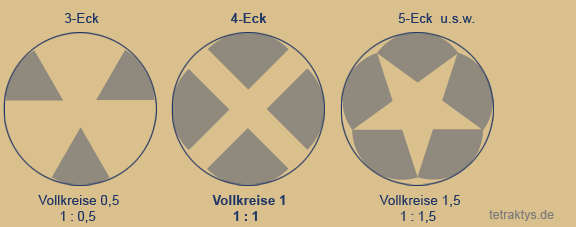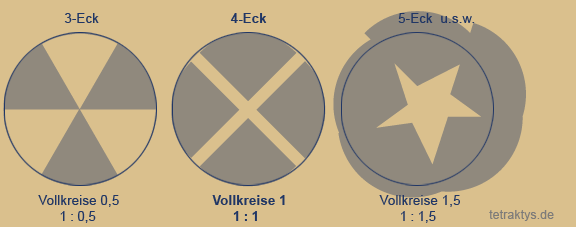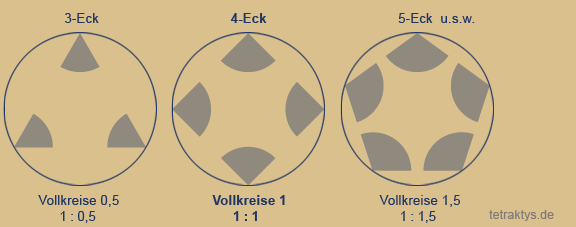
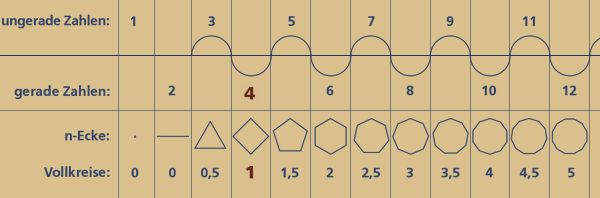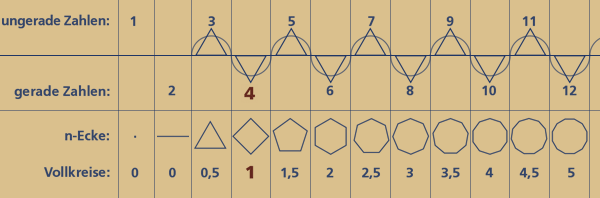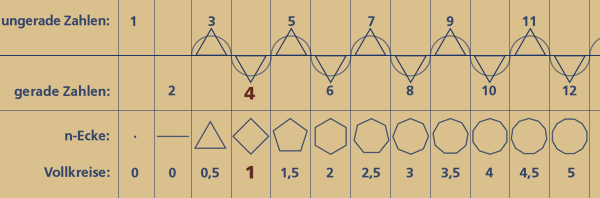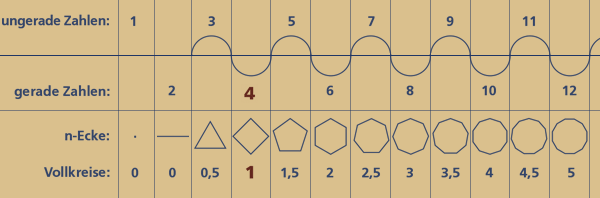
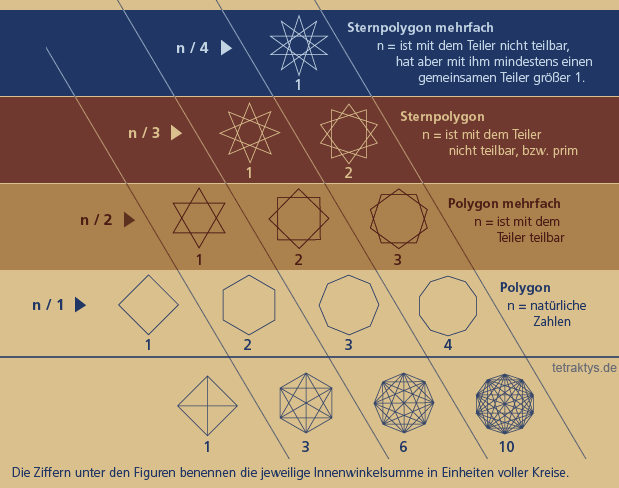
Auch die Abfolge der natürlichen Zahlen enthält exakt diese zwingend 4-gliedrige Drehmatix, sobald wir die Zahlenwertsymbole unseres Dezimalsystems durch Polygone (n-Ecke) bzw. Punktemengen ersetzen. Die Punktemenge 3 – dargestellt als Dreieck, hat zum ersten Mal die Innenwinkelsumme eines halben Kreises (180 Grad). Nur ein Punkt bzw. eine Ecke mehr macht aus einem halben Kreis einen Vollkreis.
Das 4-Eck (4x90 Grad) hat also die Winkelsumme eines vollen Kreises.
Damit ist das Vier(!)-eck (Tetraktys = Vierheit) auch das einzige Polygon mit dieser Eigenschaft. Beim Fünfeck beträgt die Innenwinkelsumme schon 1,5 Vollkreise, beim 6-Eck 2 Vollkreise usw...
Demzufolge beginnen alle ungeraden Punktemengen mit einem neuen nur halben Kreis bzw. Dreieck, welcher mit jedem darauf folgenden Punkt zu einem Vollkreis bzw. Viereck vervollständigt wird.
Die "abschließende" Zahl ist also immer eine gerade Zahl.
Zu einem vollen Kreis gehören immer zwei Punkte bzw. Zahlen, die tatsächlich auch wieder zwei Dreiecken entsprechen, da sich mit jedem neuen Punkt auch ein neues Dreieck aufspannt:
An dieser Gesetzmäßigkeit wird u. a. auch verständlich, warum die Pythagoreer und Platoniker den ungeraden Zahlen männlich, schöpferische Eigenschaften zugeschrieben haben, den geraden Zahlen dagegen weiblich, erhaltende Eigenschaften.
Diese Abbildung auf einer rosenkreuzerischen Publikation des 18. Jhdt. zeigt ein Symbol, welches die alchemistische Doppel-Ouroboros mit dem Freimaurersymbol von Winkelmaß und Zirkel kombiniert. Das Ouro (Schwanz) Boros (Essen) (Der den Schwanz isst) geht zurück auf die Ägypter und gegebenenfalls weiter zurück nach Babylon und den Sumerern. Auch in Griechenland, China, Indien, Japan und dem nahen Osten ist dieses Symbol zu finden. Freimaurer und Theosophische Gesellschaften verweisen ebenfalls auf dieses Symbol für Unendlichkeit. Es stellt das "Wie oben, so unten" Konzept dar. Der Ouroboros steht außerdem für Ewigkeit, Winter /Sommer-Sonnenwenden, Reinkarnation, Unsterblichkeit,die Zyklen des Universums und des Lebens selbst. Der Doppel-Ouroboros ist insbesondere ein Doppelwesen aus Drache und Schlange. Dies beinhaltet auch die Konzepte von Himmel und Erde, sowie Geist und Körper. Die Freimaurersymbole Winkelmaß und Zirkel sind diesen Entsprechungen analog. Der Zirkel steht für das männlich aktive, der Winkel für weiblich passive Prinzip.
Speziell die Kombination von Doppel-Ouroboros, Winkelmaß und Zirkel, sowie die zwei ineinander verschränkten Dreiecke umschreiben in nahezu perfekter Detailtreue die oben beschriebenen Gesetzmäßigkeiten im "Geometrie-Zahlenstrahl"
Tatsächlich beinhalten nur die geradzahligen Polygone rechte Winkel, ungeradzahlige keinen einzigen. Denn alle Sternpolygone (entsprechend den Teilereigenschaften von Mengen), die sich in die geradzahligen Polygone bis unendlich einbeschreiben lassen, enthalten auch parallel laufende Tangenten, da nur geradzahlige Polygone Eckpunkte aufweisen, die sich gegenüber stehen.
Näheres dazu in: Tetraktys.de
Das Wissen um diese Drehmatrix im "Geometrie-Zahlenstrahl" macht auf eindrucksvolle Weise verständlich, warum die Pythagoreer ihre "Zahlenmystik" auf den Kosmos übertrugen.
Auch das Yin und Yang beinhaltet zwei statische und zwei dynamische Phasen.
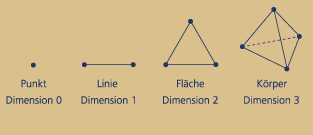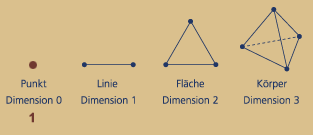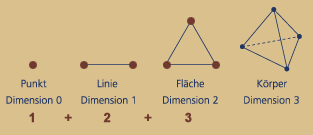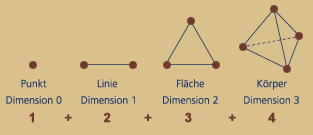
Punkt - Linie - Fläche - Körper
All die zyklischen Kreisläufe im Kosmos und auf der Erde, sowohl in der belebten als auch unbelebten Natur sind der oben beschriebenen viergliedrigen Periodizität von Kreisbewegungen unterworfen.
Aufstieg, Höhepunkt, Abstieg, Ruhephase.
oder direkt auf ein Lebewesen übertragen:
Geburt, Fortpflanzung, Alter, Tod.
Diese Kreisbewegung lässt sich unterteilen in ein aktives und passives Dreieck, entsprechend einer Sinuskurve. Beide Dreiecke zusammen ergeben wieder ein Viereck mit der Winkelsumme eines vollen Kreises. Auch der geometrisch dargestellte Zahlenstrahl enthält eine viergliedrige Drehmatrix, welche mit Punkt Linie, Dreieck und Quadrat beginnt, um sich sodann bis unendlich mit Dreieck und Quadrat zu wiederholen.
Wie aber könnte man den leeren Raum definieren, in dem all diese Kreisläufe stattfinden?
Oder wie kann man sich den unendlichen Raum bzw. das Vakuum vorstellen? Wenn von einem Mittelpunkt ausgehend alle Richtungen gleich unendlich lang sind, so entspricht der unendliche Raum ganz zweifellos einer Kugel.
Da in einem unendlichen Raum jeder Punkt auch Mittelpunkt ist, sollte jeder dieser Punkte die exakt selben Eigenschaften seiner Nachbar-Punkte haben, so dass der Raum in sich selbst eine Einheit bildet. Diese Bedingung ist tatsächlich auch erfüllt, wenn man den leeren Raum mit exakt gleich großen Kugeln füllt, so dass sich alle Kugeln dicht an dicht gegenseitig berühren.
Verbindet man nun gedanklich alle Mittelpunkte der Kugeln miteinander, so erhält man eine homogene Gitterstruktur, die lediglich aus Dreieck- und Quadrat-Flächen besteht (platonische Parkettierungen), welche sich wieder nur aus pyramidenförmigen Zellen (Tetraeder-, Oktaeder-Lücken) bildet.
Dies sind die sogenannten kubischen Kristallsysteme, die in der Kristallographie von größter Bedeutung sind. Denn die Anordnung von Atomen in einer dichtesten Kugelpackung entspricht einem wichtigen Grundprinzip bei der Bildung von Kristallen: die Minimierung des Volumens.
Nicht nur naturwissenschaftlich, sondern auch philosophisch (von Platon über Johannes Kepler bis Buckminster Fuller) war diese Kristallstruktur von jeher bedeutend.
Hier wird dieses Thema ausführlicher behandelt: Die Geometrie des lückenlosen Raumes
So definieren sich also sowohl der leere "statisch kristalline" Raum, als auch die dynamischen Kreisläufe im Raum selbst mit der Vierheit von Punkt, Linie, Dreieck und Quadrat.
Auf diese Weise herrscht die Tetraktys sowohl über die Zeit als auch über den Raum.
Punkt - Linie - Fläche - Körper – Die Tetraktys in Samuel Prichards "Masonry Dissected"
Masonry Dissected (engl.), "Zergliederte Freimaurerei", Verräterschrift von Samuel Prichard, die 1730 in London und nachher in einer Reihe von Übersetzungen erschien und zum erstenmal ausführlich das freimaurerische Brauchtum der Öffentlichkeit bekannt machte.
In diesem Frage-Antwort-Stück wird direkt auf die Pythagoreische Tetraktys von Punkt, Linie, Fläche und Körper Bezug genommen. Ein deutlicher Hinweis darauf, dass zumindest in den Anfängen der Freimaurerei pythagoreisch, platonisches Gedankengut einen ziemlich hohen philosophischen Stellenwert hatte.
Im Folgenden also die wichtigen Textpassagen, die aus Platzgründen hier natürlich aus dem
inhaltlichen Zusammenhang gerissen sind. Die erste Passage ist ein Fragestück für den Freimaurer-Lehrling:
F.: Wie manche Gründe sind in der Maurerey?
A.: Vier.
F.: Welche sind es?
A.: Punct, Linie, Oberfläche und das Dichte. (Solidum)
F.: Erkläret selbige?
A.: Punct ist das Centrum, um welches der Meister nicht irren kann; Linie ist die Länge ohne Breite; Oberfläche ist die Länge und Breite; Solidum begreifet das Ganze.
Dieser zweite Textausschnitt ist dem Fragestück im Bezug auf den Gesellengrad entnommen:
Die Wissenschaften sind aus Versen von edler Einrichtung zusammen gesetzet; ein Punct, eine Linie und eine Oberfläche, aber ein Solidum ist das Letzte.
Gottes guten Gruß zu dieser unserer glücklichen Zusammenkunft.
"Die Zehnzahl" – aus: "Von den pythagoreischen Zahlen"
Quelle: "Die Vorsokratiker" von Wilhelm Capelle, Alfred-Kröner-Verlag Leipzig 1935
I Zahlenlehre
Archytas und Philolaos nennen ohne Unterschied das Eine auch Monade und die Monade Eins.
[Theon von Smyrna S. 20, 19 Hiller = 44 A 10]
Einige haben auch die »Vierheit« — bei der ihr gewaltigster Eid ist — die nach ihrer Meinung die vollkommenste Zahl. d. h. die Zehnzahl, zustande bringt, als Urgrund der Gesundheit erklärt. Zu diesen gehört auch Philolaos.
[Lukian, Vom Ausgleiten beim Tanz 5 = 44 A 11]
Speusippos, Sohn von Platons Schwester Potone, sein Nachfolger als Haupt der Akademie vor Xenokrates, hat aus den stets mit besonderem Eifer gepflogenen pythagoreischen Erörterungen, vor allem aus den Schriften des Philolaos, ein hübsches Büchlein zusammengestellt, dem er den Titel »Von den pythagoreischen Zahlen« gegeben hat. Zuerst behandelt er hierin, vom Anfang bis zur Mitte, eingehend die Zahlen, die sich auf Linien beziehen, und solche, die sich auf Vielecke und allerlei Flächengebilde beziehen, und zugleich solche, die zu festen Körpern in Beziehung stehen; Dann spricht er von den fünf Figuren, die den Elementen des Kosmos zugeschrieben werden, sowie über ihre Eigentümlichkeit und ihre gemeinsamen Beziehungen, analoge und nicht analoge Verhältnisse <zwischen ihnen>.
Danach widmet er die zweite Hälfte seines Buches der Zehnzahl, indem er sie als die natürlichste und vollkommenste von allen Dingen erweist, die gleichsam kunstgemäßes Urbild für die kosmischen Schöpfungen aus sich selber (und nicht <nur> auf Grund unserer Meinungen oder Einfälle) ist und als vollkommenstes Vorbild dem das Weltganze gestaltenden Gott vor Augen steht.
Er spricht folgendermaßen über sie:
»Es ist aber die Zehn die vollkommene Zahl, und mit Recht und ganz natürlicherweise begegnen wir <Menschen> uns in dieser, Griechen und alle Völker, die auf alle mögliche Art zählen, indem wir selber dabei nichts mit Absicht tun. Denn sie hat viele Eigentümlichkeiten, wie das bei einer so vollkommenen Zahl in der Ordnung ist; viele Eigenschaften aber sind ihr nicht spezifisch eigentümlich; sie muß aber <auch> diese als vollkommene Zahl besitzen.
Erstens nun muss sie eine gerade Zahl sein, damit in ihr in gleicher Weise die ungeraden und die geraden Zahlen enthalten sind und nicht solche, die Produkte aus ungleichen Faktoren sind.
Denn da stets die ungerade Zahl früher als die gerade ist, wird, wenn nicht die schließende Zahl gerade wäre, die andere mehr haben.
Sodann muss sie die ersten und unzusammengesetzten und die zweiten und zusammengesetzten in gleicher Weise enthalten.
Das aber ist bei der Zehnzahl der Fall, dagegen bei keiner andern Zahl, die kleiner ist als zehn, wohl aber bei größeren, aber Grundzahl von ihnen ist die Zehnzahl. Und sie hat als erste, die diese Eigenschaft hat, und als die kleinste von denen, die diese Eigenschaft haben, eine gewisse Vollendung, und das ist ihr gewissermaßen eigentümlich, dass in ihr als erster unzusammengesetzte und zusammengesetzte Zahlen in gleicher Anzahl zur Erscheinung kommen.«
[Jamblich, Theologische Zahlenlehre S. 82, 10 de Falco = 44 A 13]
Wo dieses "Büchlein" von Speusippos geblieben ist oder ob es überhaupt noch existiert, darüber herrscht leider Unklarheit.
Geometrische Darstellung des beschriebenen Sachverhalts
"die ersten und unzusammengesetzte und die zweiten und zusammengesetzten"
gemäß den Teiler-Eigenschaften der Menge 10:
Details unter: Antikes Quellmaterial und: Der Schlüssel zur Tetraktys
Allgemeine Einführung:
Die Tetraktys in Johann Gottfried Herders Werk: Metakritik zur Kritik der reinen Vernunft, Leipzig 1799
"Dies Vierfache ist ein Actus der Seele; wer diese Tetraktys trennt, vernichtete das Wesen des menschlichen Verstandes".
Mit diesem rätselhaften Schlüsselsatz bezeichnet Herder seine zentrale viergliedrige Kategorienformel in Anlehnung der pythagoreischen Tetraktys, die er seiner kantkritischen Metakritik zugrundelegt.
In ihr sieht er sozusagen die Formel des "göttlichen Erkennens", die Grundlage des menschlichen Geistes und seine Wechselbeziehungen zu seiner Umwelt, als auch die Ursache des "Systems lebendiger Kräfte". Dieses viergliedrige Kategorienschema besteht aus einer Ursache, einem Gegensatzpaar und einer daraus resultierenden Synthese. Dieses symmetrische Grundschema in Form eines gleichschenkligen Kreuzes kann dann wahlweise mit analogen Begrifflichkeiten belegt werden.
Herder weist dabei auf die starken Parallelen zwischen der Tetraktys und der Kabbala (zehn Sephirot in den vier Welten) hin. Das Sephiroth-Schema des kaballistischen Baumes wird von Herder seinem viergliedrigen Kategorienschema gegenübergestellt, welches er durchaus dem symbolphilosophischen Arsenal der pythagoreisch-platonischen Tradition gleichstellt bzw. entnommen hat. Der Sepher Jezirah, das "Buch der Schöpfung" in der Kabbala und die pythagoreische Tetraktys sind ohnehin zwei Seiten der gleichen Medaille. Beide beanspruchen für sich, das Grundprinzip der göttlichen Schöpfung zu sein, und beiden liegt ein viergliedriges System zugrunde, welches in einer Zehnheit gipfelt.
Johann Gottfried Herder war nicht der Erste, der die Wesensgleichheit beider Systeme erkannte. Schon Johannes Reuchlin verglich in seinem 1494 erschienenen Werk De verbo mirifico (Über das Wunder wirkende Wort) das Tetragramm, das den Gottesnamen JHWH darstellt, mit der Tetraktys.
Studie über Johann Gottfried Herders Werk: Metakritik zur Kritik der reinen Vernunft, Leipzig 1799 "Heilige Tetraktys, Herders metakritische Hermetik" von Florian Mayr Novalis-Verlag (10. Oktober 2006) ISBN-10: 3907260406 ISBN-13: 978-3907260401

Die Tetraktys in der Musiktheorie
Sucht man nach Aufzeichnungen und Überlieferungen über Pythagoras im Zusammenhang mit seiner Tetraktys, so wird man mit Sicherheit auf ein Gemälde von Raffael treffen: "Die Schule von Athen". Dieses Kunstwerk entstand 1510, also rund 2000 Jahre nach Pythagoras. Da aber in diesem Frekso viele spekulative Betrachtungen über die Tetraktys ihren Ursprung haben, darf es nicht unerwähnt bleiben. Der Titel des Bildes verweist auf die herausragende philosophische Denkschule des antiken Griechenlands, verkörpert von ihren Vorläufern, Hauptvertretern und Nachfolgern. Im Zentrum stehen die Philosophen Platon und Aristoteles.
Das Bild ist in drei Hauptgruppen aufgeteilt:
Oben in der Mitte: die Platon-Gruppe
Links unten: die Pythagoras-Gruppe
Rechs unten: die Euklid-Gruppe
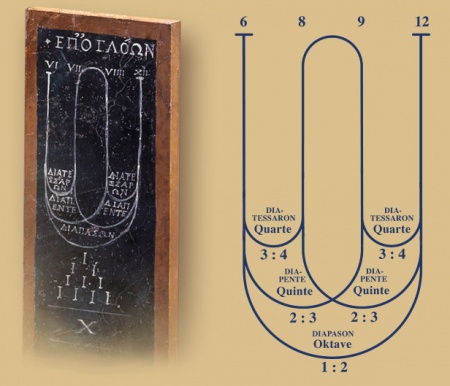
Wenden wir uns also der Pythagoras-Gruppe zu. Die sitzende Person in der Mitte stellt Pythagoras dar. Er schreibt in einem Buch, während ihm einer seiner Schüler eine schwarze Tafel reicht, auf dem mit weißer Kreide eine schleifenförmige Zeichnung zu erkennen ist. Direkt unter dieser Zeichnung ist in der Anordnung des Punktedreiecks und in römischen Ziffern 1+2+3+4=10 geschrieben.
Die wichtigste Frage, die sich nun jedem Betrachter aufdrängen muss: Woher hatte Raffael Kenntnisse über die Pythagoreer und Ihre geheimen Lehren? Da die Pythagoras-Gruppe eine der drei Hauptgruppen auf diesem Bild stellt, muss man vermuten, dass Raffael um die große Bedeutung des Pythagoras und seine Lehren in der griechischen Geisteswelt ahnte oder wusste.
Wie also wurde bisher diese Zeichnung auf der schwarzen Tafel von Kunsthistorikern und Musiktheoretikern ausgedeutet und was stellt dieses Schleifendiagramm überhaupt dar? Pythagoras gilt als Begründer der mathematischen Musiktheorie der Griechen. Die Siebenstufigkeit der Skala, die Bestimmung der Tonverhältnisse nach Quinten und Quarten wird ihm von der Musikgeschichte zugeschrieben.
Dass dieses Schleifendiagramm eine musiktheoretische Bedeutung hat, darüber besteht kein Zweifel.
Die griechischen Bezeichnungen auf der Tafel entstammen der Harmonielehre. Die Überschrift lautet übersetzt: "Das Ganze und ein Achtel", womit die Oktave gemeint ist. In den Schleifen selbst befinden sich drei weitere Begriffe: Oktave, Quinte und Quarte.
Die oberen römischen Ziffern: 6, 8, 9, 12 werden von Musiktheoretikern den ersten vier Zahlen der Obertonreihe zugeordnet. Diese stellen eine Vierheit dar:
Prime (Frequenzverhältnis 1:1)
Oktave (Frequenzverhältnis 1:2 bzw. 6:12)
Quinte (Frequenzverhältnis 2:3 bzw. 6:9 und 8:12)
Quarte (Frequenzverhältnis 3:4 bzw. 6:8 und 9:12)
Was haben nun diese harmonikalen Verhältnisse mit dem ganz oben beschriebenen Sachverhalt im Zusammenhang mit der Menge 10 und den Dimensionssprüngen zu tun?
Die Antwort ist nicht ganz einfach zu verstehen und soll hier nur grob skizziert werden:
Das wichtigste Diagramm der Musiktheorie ist das so genannte Lambdoma. Es handelt sich dabei um ein Koordinatensystem deren X- und Y-Achse jeweils einem schlichten n-Mengenstrahl entsprechen, wobei die Koordianten die jeweiligen Quotienten ergeben. Es handelt sich dabei also um eine einfache Divisionstabelle. Sowohl die X-Y-Zahlengeraden als auch alle Positionen im Koordinatensystem können als Polygone und Sternpolygone dargestellt werden.
Auch die harmonikalen Verhältnisse: 1:2, 2:3 und 3:4 lassen sich als so genannte Gleichtonlinien in dieses Diagramm eintragen. Dabei entspricht die Gleichtonlinie der Oktave bis unendlich Sternen, die aus Linien zusammengesetzt sind, die Quinte entspricht bis unendlich Symmetrien, die sich aus Dreiecken zusammensetzen, die Quarte hingegen ist aus Quadraten zusammengesetzt.
Somit finden wir auch in der Musik die Tetraktys von Punkt, Linie, Dreieck und Quadrat.
Polygone und Sternpolygone sind demnach als Schwingungsform zu begreifen.
Das Lambdoma ist sehr alt. Albert von Thimus (1806-1878) entdeckte ein bis dahin unverstandenes Zitat in einem Kommentar von Jamblichos (neuplatonischer Philosoph 3. Jh. n. Chr.) zur kleineren Arithmetik des Nikomachos (neuplatonischer Philosoph 2. Jh. n. Chr). Dort heißt es :
"Von der Einheit aus wird von einem Winkel aus eine Figur in Gestalt des Lambda gezeichnet. Auf der einen Seite der Reihe werden die an die Einheit sich anschließenden Zahlen aufgezeichnet. Die andere Seite wird - beginnend von dem größten der Teile, welcher das seiner Größe nach dem Ganzen zunächst liegende Halbe ist - der Reihe nach mit den hieran sich anschließenden Teilen beschrieben."
Diese Hinweise, wie auch das Originalzitat ist in Hans Kayers Lehrbuch der Harmonik zu finden.
(Kayser, Hans; Lehrbuch der Harmonik; Zürich, Occident, 1950, S. 60)
Siehe auch
- En:Tetractys
- Pythagoras
- Geometrie
- Geometrie? Fragen & Antworten
- Pentagramm
- Hexagramm
- Harmonik
- Melencolia § I
- Melancholia
- 500 Jahre "Melencholia 1"
- Kubus und Pyramide – der lückenlose Raum
Links
- Thema "Geometrie" auf Tetraktys.de http://tetraktys.de/einfuehrung-1.html#bedeutung-1