Pentagramm: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 6: | Zeile 6: | ||
[[Bild:tetraktys-simplex-2.gif|thumb|300px|Simplex des 5-Ecks, diese Figur entspricht einem Tetraeder der 4. Dimension. Animation der Drehbewegung des Pentagramms im Fünfeck. Es finden 2 Kreisumdrehungen statt.]] | [[Bild:tetraktys-simplex-2.gif|thumb|300px|Simplex des 5-Ecks, diese Figur entspricht einem Tetraeder der 4. Dimension. Animation der Drehbewegung des Pentagramms im Fünfeck. Es finden 2 Kreisumdrehungen statt.]] | ||
| − | |||
| − | |||
== Pentagramm oder Pentalpha == | == Pentagramm oder Pentalpha == | ||
Version vom 23. April 2019, 21:04 Uhr
Inhaltsverzeichnis
Pentagramm oder Pentalpha
Quelle: Lennhoff, Posner, Binder
Drudenfuß das aus den Diagonalen oder aus der Verlängerung der Seiten eines Fünfecks entsteht, bezw. aus fünf Alphas gebildet wird, hat von altersher symbolische Bedeutung. Bei den Pythagoräern war es ein Gruß- oder Erkennungszeichen, wobei fünf Buchstaben, die "sei gesund !" bedeuteten, die fünf Ecken zierten. Das Pentagramm wird auch in Zusammenhang mit dem "Siegel Salomonis" gebracht, da der König es auf dem Grundstein des Tempels angebracht habe.
In Goethes "Faust" verhindert es, nach altem Brauch auf die Schwelle gezeichnet, den Eintritt des Bösen, insoferne nicht die Spitze nach außen offen ist. In vielen freimaurerischen Systemen steht im Pentagramm ein G. umfaßt vom flammenden Stern. (Vergl. Henne am Rhyn, "Symbolik".)
Das Pentagramm in der Geometrie und in der Zahlenthorie
Quelle: SIMPLEX – DER FESTE AGGREGATZUSTAND DER ZAHL http://tetraktys.de/geometrie-2.html
Das Pentagramm ist wie auch das Hexagramm Teil einer Drehmatrix, identisch mit den Teilereigenschaften von Mengen. Die geometrisch arithmetische Aussage lautet:
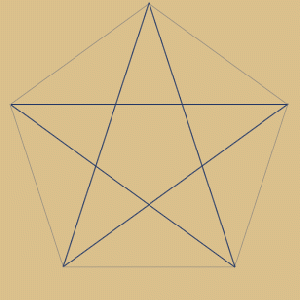
5 geteilt durch 2 gleich 2,5. Bezw. 2 mal 2,5. Nur jeder zweite Punkt des Fünfecks ist verbunden. Auf diese Weise muss das 5-Eck zweimal umrundet werden, bis sich die Sternfigur schließt.
Das Pentagamm ist die erste Sternfigur, welche folgende arithmetische Eigenschaft aufweist: Die natürliche Zahl (in diesem Fall Menge 5) ist mit der Teilermenge (in diesem Fall Menge 2) nicht teilbar.
Des Weiteren ist das Fünfeck (und der Fünfstern) das erste regelmäßige Polygon, welches nicht mit sich selbst in der Ebene und im Raum lückenlos parkettierbar (im weitesten Sinne kompatibel) ist.
Siehe Platonische Parkettierungen https://de.wikipedia.org/wiki/Parkettierung#Platonische_Parkettierungen
Das Fünfeck-Simplex, zusammengesetzt aus einem Fünfeck und einem Pentagramm, ist ein Tetraeder der 4. Dimension. Die genaue Bezeichnung ist 4-Simplex.
Aus diesen arithmetischen und geometrischen Eigenschaften innerhalb systematischer Zusammenhänge lassen sich auch die philosophischen Interpretationen des Pentagramms als Stern des "Mikrokosmos" in der Zahlenmystik der Hermetik und auch in der Freimaurerei herleiten.
Siehe auch
Links
Wikimedia Commons (public domain) by AnonMoos *https://commons.wikimedia.org/wiki/File:Double-interlaced-pentagram.svg
