Harmonik: Unterschied zwischen den Versionen
K (→Videos) |
Admin (Diskussion | Beiträge) K (Textersetzung - „</videoflash>“ durch „</youtube>“) |
||
| (9 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[Datei:Ulm1.jpg|thumb| | + | [[Datei:Banner8.jpg|thumb|835px|HARMONIK-SYMPOSIUM AM 23/24. APRIL 2016 IN NÜRNBERG, DAS THEMA LAUTET: "DER MENSCH IM KOSMOS". GÄSTE SIND HERZLICH EINGELADEN. Kontakt: [http://harmonik-zentrum-deutschland.de/ Harmonik-Zentrum-Deutschland]]] |
| − | [[Datei:Berliner Werkstatt5.jpg|thumb| | + | |
| − | [[Datei:HA119.jpg|thumb| | + | == Harmonik == |
| + | |||
| + | [[Datei:Ulm1.jpg|thumb|right|350px|[[Pythagoras]] im Chorgestühl des Ulmer Münsters. Foto: [[Tomas Ostermann]]]] | ||
| + | |||
| + | [[Datei:Berliner Werkstatt5.jpg|thumb|350px|right|Vortrag über Harmonik in der [[Berliner Werkstatt]]]] | ||
| + | |||
| + | [[Datei:HA119.jpg|thumb|350px| Mit bestechender Klarheit konfrontiert uns die Autorin in ihrem ersten Buch mit einer bereits im Altertum bekannten, durch Naturbeobachtung entstandenen geheimnisvollen Lehre der Harmonik, deren konkrete Auswirkungen wir täglich erleben können. Sie hat unsere abendländische Kultur stärker beeinflusst als die Stilepochen der letzten zweitausend Jahre, obwohl in der Gegenwart kaum Notiz von ihrer elementaren Wirkungskraft genommen wird. | ||
Wie die großen griechischen Mathematiker, die mit Diagrammen und Zeichnungen Erkenntnisse "begreifbar" machten, nutzt auch Henny Jahn diese Möglichkeit des Erkenntnisgewinns, um die Leser mit dieser einzigartigen Wissenschaft vertraut zu machen. Darüber hinaus gibt Jahn dem Leser Anregungen, selbst aktiv zu werden. | Wie die großen griechischen Mathematiker, die mit Diagrammen und Zeichnungen Erkenntnisse "begreifbar" machten, nutzt auch Henny Jahn diese Möglichkeit des Erkenntnisgewinns, um die Leser mit dieser einzigartigen Wissenschaft vertraut zu machen. Darüber hinaus gibt Jahn dem Leser Anregungen, selbst aktiv zu werden. | ||
| Zeile 31: | Zeile 37: | ||
u.v.a.m. Bestellung: [[SCHOPF]]]] | u.v.a.m. Bestellung: [[SCHOPF]]]] | ||
| − | + | [[Datei:HA138.jpg|thumb|350px|Eine Zusammenstellung kleinerer Texte zur Harmonik. Zahlenharmonikale Untersuchungen von zu den Tempeln von Paestum und zum Pythagoreischen Dreieck. Sehr geeignet als erste Einführung in die Harmonik mit dem Schwerpunkt auf der Kayserschen Harmonik. | |
| − | [[Datei:HA138.jpg|thumb| | ||
Über den Autor: | Über den Autor: | ||
| Zeile 54: | Zeile 59: | ||
== Der Begriff "Harmonik" speziell in der Musiktheorie == | == Der Begriff "Harmonik" speziell in der Musiktheorie == | ||
| + | |||
Harmonik (von lat.-griech. harmonia = „Zusammenfügung, Einklang“) ist ein umfassender Begriff aus der Musiktheorie und -praxis; er steht für den Zusammenklang der Töne, also für die vertikale Komponente der Musik. | Harmonik (von lat.-griech. harmonia = „Zusammenfügung, Einklang“) ist ein umfassender Begriff aus der Musiktheorie und -praxis; er steht für den Zusammenklang der Töne, also für die vertikale Komponente der Musik. | ||
| Zeile 65: | Zeile 71: | ||
Mit Harmonielehre wird allerdings nur ein Teilaspekt der Musikgeschichte – nämlich die Harmonik – unter satztechnischen und analytischen Gesichtspunkten erfasst. Harmonielehre bedeutet vor allem, aus einer pädagogischen Absicht heraus eine Handwerkslehre zu vermitteln, die zu gewissen Abstraktionen und Vereinfachungen führen muss, da eine stilistische Entwicklung von über 300 Jahren zu berücksichtigen ist. Dennoch kommt der Harmonielehre noch heute eine zentrale Bedeutung zu, da sie Einblick in stilistische – und damit interpretatorische – Grundfragen der Musik zwischen 1600 und 1900 gibt. Darüber hinaus sind Grundkenntnisse von Harmonielehre auch für das Verständnis der sog. Populärmusik oder des Jazz unabdingbar. Quelle: [http://freimaurer-wiki.de/index.php/Freimaurer-wiki:Aktuelle_Ereignisse#Grunds.C3.A4tzliches Wikipedia] | Mit Harmonielehre wird allerdings nur ein Teilaspekt der Musikgeschichte – nämlich die Harmonik – unter satztechnischen und analytischen Gesichtspunkten erfasst. Harmonielehre bedeutet vor allem, aus einer pädagogischen Absicht heraus eine Handwerkslehre zu vermitteln, die zu gewissen Abstraktionen und Vereinfachungen führen muss, da eine stilistische Entwicklung von über 300 Jahren zu berücksichtigen ist. Dennoch kommt der Harmonielehre noch heute eine zentrale Bedeutung zu, da sie Einblick in stilistische – und damit interpretatorische – Grundfragen der Musik zwischen 1600 und 1900 gibt. Darüber hinaus sind Grundkenntnisse von Harmonielehre auch für das Verständnis der sog. Populärmusik oder des Jazz unabdingbar. Quelle: [http://freimaurer-wiki.de/index.php/Freimaurer-wiki:Aktuelle_Ereignisse#Grunds.C3.A4tzliches Wikipedia] | ||
| + | |||
== Pythagoräer == | == Pythagoräer == | ||
| + | |||
Nach Auffassung der Pythagoräer stand eine mathematische Ordnung oder noch präziser ausgedrückt, die Zahl, in unmittelbarem Zusammenhang mit jeder Form von Musik, weil jeder Ton eine ganz bestimmte, auch mathematisch darstellbare Schwingungsfrequenz hat. Dieser Zusammenhang zwird plausibel, wenn man sich vergegenwärtigt, dass die Intervalle innerhalb der Tonleiter als Verhältnisse ganzer Zahlen ausdrückbar sind. | Nach Auffassung der Pythagoräer stand eine mathematische Ordnung oder noch präziser ausgedrückt, die Zahl, in unmittelbarem Zusammenhang mit jeder Form von Musik, weil jeder Ton eine ganz bestimmte, auch mathematisch darstellbare Schwingungsfrequenz hat. Dieser Zusammenhang zwird plausibel, wenn man sich vergegenwärtigt, dass die Intervalle innerhalb der Tonleiter als Verhältnisse ganzer Zahlen ausdrückbar sind. | ||
| Zeile 118: | Zeile 126: | ||
== Videos == | == Videos == | ||
| − | |||
| + | <youtube>mOJPyhfdXhs</youtube> | ||
| − | < | + | <youtube>cauccq04Cn0</youtube> |
| − | |||
| − | |||
| − | + | Harmonikale Grundlagen und Lambdoma von Henny Jahn. | |
| − | |||
| + | <youtube>4obreB4UUYY</youtube> | ||
| + | <youtube>UnO4ZzgR-zg</youtube> | ||
Henny Jahn, Orgelbauerin und Autorin des Buches "Weltformel Lambdoma" erklärt an Hand verschiedener Lambdoma-Grafiken nicht nur musiktheoretische Zusammenhänge, sondern regt an darüber nachzudenken, dass hinter dieser Zahlen-Matrix sehr viel mehr steckt, als nur ein paar Noten. | Henny Jahn, Orgelbauerin und Autorin des Buches "Weltformel Lambdoma" erklärt an Hand verschiedener Lambdoma-Grafiken nicht nur musiktheoretische Zusammenhänge, sondern regt an darüber nachzudenken, dass hinter dieser Zahlen-Matrix sehr viel mehr steckt, als nur ein paar Noten. | ||
| Zeile 143: | Zeile 150: | ||
Die einzelnen Positionen innerhalb des Koordinatensystems zeigen die daraus resultierenden, jeweiligen Zahlenbrüche. | Die einzelnen Positionen innerhalb des Koordinatensystems zeigen die daraus resultierenden, jeweiligen Zahlenbrüche. | ||
Die namensgebende dreieckförmige Darstellung des Lambdomas (benannt nach dem griechischen Buchstaben Lambda) soll die ihm innewohnende Symmetrie anschaulich machen. | Die namensgebende dreieckförmige Darstellung des Lambdomas (benannt nach dem griechischen Buchstaben Lambda) soll die ihm innewohnende Symmetrie anschaulich machen. | ||
| − | |||
== „Sphärenmusik" == | == „Sphärenmusik" == | ||
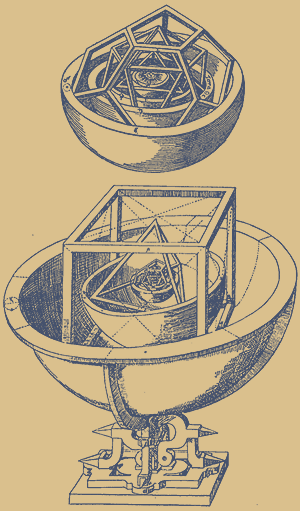
| − | [[Datei:Sphaeren-keppler.gif|thumb| | + | [[Datei:Sphaeren-keppler.gif|thumb|350px|Abb. "Planetensphären" nach dem Vorbild der platonischen Körper, aus "Harmonices Mundi" von Johannes Kepler]] |
In der Geistesgeschichte der Menschheit lebt seit mehreren Jahrtausenden die Vorstellung von einem harmonisch geordneten Kosmos. Pythagoras vermochte der Legende nach, die „Sphärenmusik" zu erlauschen. | In der Geistesgeschichte der Menschheit lebt seit mehreren Jahrtausenden die Vorstellung von einem harmonisch geordneten Kosmos. Pythagoras vermochte der Legende nach, die „Sphärenmusik" zu erlauschen. | ||
| Zeile 166: | Zeile 172: | ||
Warum haben Kepler – und vor allem auch die Pythagoreer – die Platonischen Körper so fasziniert, dass sie versuchten, diese Symmetrien der 5 vollkommenen Körper auf das Universum zu übertragen? | Warum haben Kepler – und vor allem auch die Pythagoreer – die Platonischen Körper so fasziniert, dass sie versuchten, diese Symmetrien der 5 vollkommenen Körper auf das Universum zu übertragen? | ||
| − | + | Hartmut Warm hat nun Kepplers Idee im weitesten Sinne wieder aufleben lassen. Allerdings geht es bei [http://www.keplerstern.de/ Hartmut Warms] Entdeckung nicht um die Abstände der einzelnen Planetenbahnen, sondern eben um die Bewegungsmuster mehrer Planeten innerhalb von bestimmten Zeitintervallen. | |
| − | == Siehe auch | + | == Siehe auch == |
*[[Geometrie]] | *[[Geometrie]] | ||
*[[Geometrie? Fragen & Antworten]] | *[[Geometrie? Fragen & Antworten]] | ||
| Zeile 174: | Zeile 180: | ||
== Links == | == Links == | ||
| − | * | + | *Harmonikzentrum Deutschland e.V. http://www.harmonik-zentrum-deutschland.de |
| − | * | + | *Tetraktys.de http://www.tetraktys.de |
| − | + | *Hartmut Warm, Keplerstern.de http://www.keplerstern.de/ | |
| + | |||
| + | [[Kategorie:Lexikon|Harmonik]] | ||
Aktuelle Version vom 20. Dezember 2020, 20:10 Uhr

Inhaltsverzeichnis
Harmonik



Was ist Harmonik?
Harmonik versteht sich als ein ganzheitliches Denk- und Erlebnisprinzip auf der Grundlage der Entsprechung von Klang, Zahl und Form im Geiste von Pythagoras, Johannes Kepler und Hans Kayser. Sie gründet sich auf wissenschaftliche Kriterien, geht aber darüber hinaus. Sie öffnet sich auch der Wahrnehmung, Erfahrung und übergreifender kultureller und sozialer Interaktion.
Diese allumfassende Sichtweise der Harmonik rührt aus jenen Zeiten her, in der sich Wissenschaften von den Religionen noch nicht gelöst hatten.
Heute haben wir die Schwierigkeit, dass der Wissenschafter von Kausalketten und Zufall spricht, der Philosoph von Sinn, der Theologe aber von göttlicher Schöpfung und Vorsehung, alle drei also eine verschiedene Sprache sprechen.
Harmonik ist eine interdisziplinäre, ganzheitliche Lehre. Sie erläutert uns prägnant, wie Mathematik, Musik, Philosophie und Theologie im Zahlenschema des Lambdomas in harmonikaler Weise verbunden sind.
Definition des Begriffs "Harmonik" von Harmonikzentrum Deutschland e.V.
Der Begriff "Harmonik" speziell in der Musiktheorie
Harmonik (von lat.-griech. harmonia = „Zusammenfügung, Einklang“) ist ein umfassender Begriff aus der Musiktheorie und -praxis; er steht für den Zusammenklang der Töne, also für die vertikale Komponente der Musik.
In der Antike deckt sich die Harmonik ganz mit der Theorie der Tonsysteme (siehe Philolaos und Aristoxenos). Seit der Entwicklung der mehrstimmigen Musik engte sich die Bedeutung der Harmonik mehr und mehr auf den gleichzeitigen Zusammenklang verschiedener Stimmen ein. In dieser heute vorherrschenden engeren Bedeutung umfasst Harmonik alle stilistischen Formen des Zusammenklangs von Musik, beginnend bei der frühen Mehrstimmigkeit des europäischen Mittelalters bis hin zu Klangstrukturen der Avantgarde. Wie die Mehrstimmigkeit ist die Harmonik daher eine primär abendländisch-europäische Entwicklung.
Unter Harmonielehre wird dagegen die systematische Erfassung der Akkordgestalten und des tonalen Klangraumes verstanden, verbunden mit methodischen Anleitungen zur fehlerfreien Handhabung der Klangverbindungen im Sinne der traditionellen Vorgaben der Musik innerhalb der dur-moll-tonalen Epoche (ca. 1600 bis in die Gegenwart).
Jean-Philippe Rameau
Der Begriff „Harmonielehre“ stützt sich auf Jean-Philippe Rameaus (1683–1764) Traité de l'Harmonie (1722), ein Traktat, welches noch während der Zeit des Generalbasses die Erkenntnisse der Fundamentalbass-Theorie zu einer mehr analytisch ausgerichteten Theorie nutzt. Die von Jacob Gottfried Weber (1779–1839) entwickelte und später von Simon Sechter (1788–1867) und Arnold Schönberg (1874–1951) ausgebaute Stufentheorie wurde gegen Ende des 19. Jahrhunderts durch die von Hugo Riemann (1849–1919) begründete Funktionstheorie ergänzt. Beide Systeme haben sich bis in die heutige Zeit mit Modifikationen und Erweiterungen erhalten. Heinrich Schenker (1868-1935) verbindet in seiner Harmonielehre die Kontrapunktlehre mit der Akkordlehre: die Stimmführung wird nunmehr als die Horizontalisierung der (vertikalen) Harmonik verstanden (bezeichnet auch als Ursatz in der von ihm begründeten Reduktionsanalyse).
Mit Harmonielehre wird allerdings nur ein Teilaspekt der Musikgeschichte – nämlich die Harmonik – unter satztechnischen und analytischen Gesichtspunkten erfasst. Harmonielehre bedeutet vor allem, aus einer pädagogischen Absicht heraus eine Handwerkslehre zu vermitteln, die zu gewissen Abstraktionen und Vereinfachungen führen muss, da eine stilistische Entwicklung von über 300 Jahren zu berücksichtigen ist. Dennoch kommt der Harmonielehre noch heute eine zentrale Bedeutung zu, da sie Einblick in stilistische – und damit interpretatorische – Grundfragen der Musik zwischen 1600 und 1900 gibt. Darüber hinaus sind Grundkenntnisse von Harmonielehre auch für das Verständnis der sog. Populärmusik oder des Jazz unabdingbar. Quelle: Wikipedia
Pythagoräer
Nach Auffassung der Pythagoräer stand eine mathematische Ordnung oder noch präziser ausgedrückt, die Zahl, in unmittelbarem Zusammenhang mit jeder Form von Musik, weil jeder Ton eine ganz bestimmte, auch mathematisch darstellbare Schwingungsfrequenz hat. Dieser Zusammenhang zwird plausibel, wenn man sich vergegenwärtigt, dass die Intervalle innerhalb der Tonleiter als Verhältnisse ganzer Zahlen ausdrückbar sind.
Nach dieser Erkenntnis kamen die Pythagoräer zu der Schlussfolgerung, dass auch alle übrigen Dinge der Natur Zahlen nachgebildet seien, dass also das Wesen aller Dinge im Prinzip aus Zahlen besteht.
Diese Theorie brachte sie schließlich zu der Erkenntnis, dass eine umfassende mathematisch-kosmische Ordnung existiert. Pythagoras brachte dieses Auffassung in seiner Lehre von der Harmonie der Sphären zum Ausdruck.
Danach verursachen alle Himmelskörper durch ihre Geschwindigkeit Geräusche einer unbeschreiblichen Stärke. Nach Pythagoras entstehen je nach Geschwindigkeit und Abstand von den anderen ganz individuelle Töne. Am Ende würde durch den Kreislauf ein überaus harmonischer Urklang entstehen. Weil jeder Mensch seit seiner Geburt dieser Planetenmelodie ausgesetzt ist, könne er diese Töne aber nicht wahrnehmen. Denen Unterschied zu der absoluten Stille könne er gar nicht erkennen.


Videos
Harmonikale Grundlagen und Lambdoma von Henny Jahn.
Henny Jahn, Orgelbauerin und Autorin des Buches "Weltformel Lambdoma" erklärt an Hand verschiedener Lambdoma-Grafiken nicht nur musiktheoretische Zusammenhänge, sondern regt an darüber nachzudenken, dass hinter dieser Zahlen-Matrix sehr viel mehr steckt, als nur ein paar Noten.
Henny Jahn will nicht belehren, sondern fordert dazu auf, die von Ihr aufgezeigten Tatsachen selbst zu überprüfen, nachzuzeichnen und nachzuempfinden, um sich von der tiefen Wahrheit zu überzeugen.
Nur so wird man Gewinn aus diesen Erkenntnissen ziehen.
Das Lambdoma
Das Lambdoma ist das wichtigste Diagramm harmonikaler Forschung. Es zeigt ein 45 Grad gekipptes Koordinatensystem, deren x- und y-Achse jeweils die Zahlengerade bis unendlich enthalten.
Die einzelnen Positionen innerhalb des Koordinatensystems zeigen die daraus resultierenden, jeweiligen Zahlenbrüche. Die namensgebende dreieckförmige Darstellung des Lambdomas (benannt nach dem griechischen Buchstaben Lambda) soll die ihm innewohnende Symmetrie anschaulich machen.
„Sphärenmusik"
In der Geistesgeschichte der Menschheit lebt seit mehreren Jahrtausenden die Vorstellung von einem harmonisch geordneten Kosmos. Pythagoras vermochte der Legende nach, die „Sphärenmusik" zu erlauschen. Seine Entdeckung, dass konsonante musikalische Intervalle einfachen Zahlenverhältnissen entsprechen, wurde u.a. von Platon auf die antiken Modelle vom Aufbau des Kosmos übertragen.
Zu Beginn der wissenschaftlich orientierten Neuzeit brachte Johannes Kepler neue Impulse in die alten intuitiven Vorstellungen; er war es, der allen moderneren Gedanken zur Sphärenharmonie das Fundament gegeben hat.
Mit Hilfe der von ihm entdeckten Planetengesetze versuchte er zu belegen, dass in den Bewegungen der Planeten Verhältnisse herrschen, die denen musikalischer Intervalle entsprechen. Das umfassende Ziel seiner „Harmonice Mundi" (Weltharmonik) aus dem Jahre 1618 bestand darin nachzuweisen, dass die Grundlagen von Geometrie, musikalischer Harmonie und Astronomie im wesentlichen eins sind oder, anders formuliert, die unterschiedlichen Seinsbereiche von den gleichen schöpferischen Prinzipien durchwirkt werden.
Das, was „die Welt im Innersten zusammenhält", sind für Kepler letztlich geometrische Urbilder: göttliche Gedanken, die dem Aufbau der Musik und des Kosmos zu Grunde liegen. Auch lange nach Kepler waren Philosophen und Dichter wie Friedrich Schelling, Hans Kayser, Goethe, Hermann Hesse u.v.a. von der grundsätzlichen Gültigkeit dieser Gedanken überzeugt. Aus heutiger wissenschaftlicher Sicht wird die „Sphärenharmonie" in unserem Sonnensystem allerdings bisher nicht allzu ernst genommen, Keplers diesbezügliche Vorstellungen werden heute als "schöne Träumerei" bezeichnet.
Denn letztendlich verwarf Kepler seine Theorie von den Abständen der 6 damals bekannten Planeten, von welchen er meinte, dass sie durch die 5 platonischen Körper bestimmt wäre.
Bleibt die Frage: Warum haben Kepler – und vor allem auch die Pythagoreer – die Platonischen Körper so fasziniert, dass sie versuchten, diese Symmetrien der 5 vollkommenen Körper auf das Universum zu übertragen?
Hartmut Warm hat nun Kepplers Idee im weitesten Sinne wieder aufleben lassen. Allerdings geht es bei Hartmut Warms Entdeckung nicht um die Abstände der einzelnen Planetenbahnen, sondern eben um die Bewegungsmuster mehrer Planeten innerhalb von bestimmten Zeitintervallen.
Siehe auch
Links
- Harmonikzentrum Deutschland e.V. http://www.harmonik-zentrum-deutschland.de
- Tetraktys.de http://www.tetraktys.de
- Hartmut Warm, Keplerstern.de http://www.keplerstern.de/